INTEGRAL
● Dari teori diferensial kita telah mengetahui,bahwa :
F(x) = x2 + 2x – 1 → f’(x) = 2x + 2
F(x) = x2 + 2x + 3 → f’(x) = 2x + 2
F(x) = x2 + 2x + 9 → f’(x) = 2x + 2
F(x) = x2 + 2x + c → f’(x) = 2x + 2
Jadi ,jika f’(x) = 2x + 2 → f’(x) = x2 + 2x +
c
(c = bilangan konstan)
Jika y = x2 + 2x + c ,maka
dy = (2x + 2) dx
y = ∫(2x + 2) dx
Jadi ∫(2x + 2) dx = x2
+ 2x + c
Secara umum dapat dituliskan :
● Cara Mengintegralkan
1.
Dengan Rumus :
Contoh
:
2. Substitusi
a)
Substitusi tanpa perubah baru
Contoh
:
a)
Substitusi dengan perubah baru
Contoh
:
3.
Integral Parsial
Rumus :
∫uv’ . dx = uv - ∫u’v
. dx
Contoh :
a.
∫sin2x . dx = ......?
Jawab : ∫sin2x . dx = ∫sin
x . sin x . dx
Misal : u = sin x → u’ = cos x
V’ = sin x → v = -cos x
∫sin2x
. dx = sin x (-cos x) - ∫-cos x . cos x . dx
= -sin x . cos x + ∫cos2x . dx
= -sin x . cos x + ∫(1 – sin2x) dx
= -sin x . cos x + ∫dx - ∫sin2x
. dx
● PENGGUNAAN INTEGRAL
1.Menghitung Luas
2. Menghitung Volume Benda Putar
3. Menghitung
Jarak dan Kecepatan









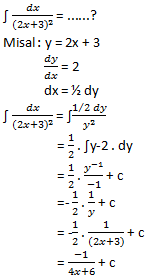






0 komentar:
Posting Komentar
Silahkan anda berkomentar, namun tetap jaga kesopanan dengan tidak melakukan komentar spam.